문제
문제 바로가기> BOJ 17485번: 진우의 달 여행 (Large)
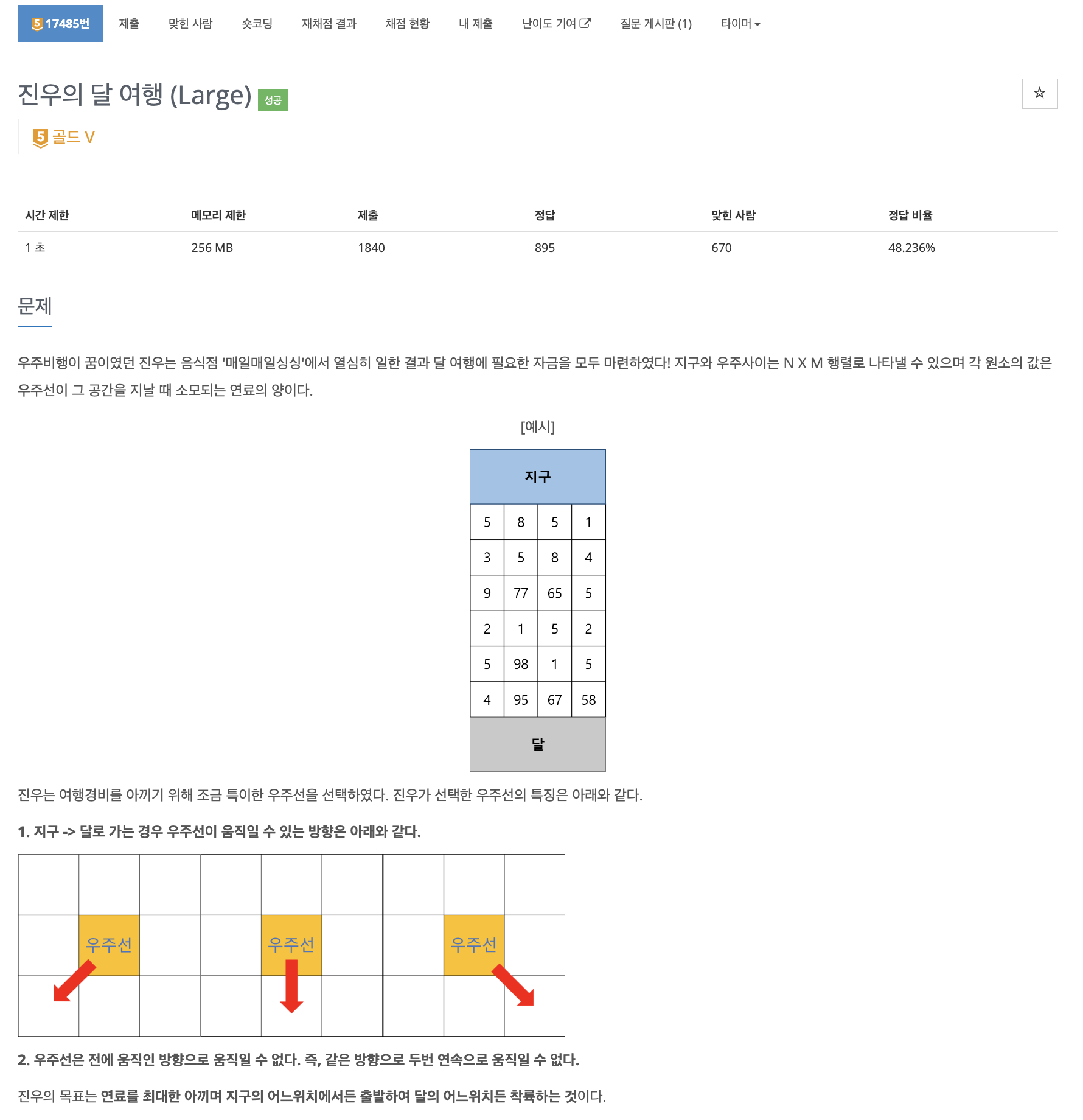
17485번: 진우의 달 여행 (Large)
첫줄에 지구와 달 사이 공간을 나타내는 행렬의 크기를 나타내는 N, M (2 ≤ N, M ≤ 1000)이 주어진다. 다음 N줄 동안 각 행렬의 원소 값이 주어진다. 각 행렬의 원소값은 100 이하의 자연수이다.
www.acmicpc.net

풀이
"달 여행에 필요한 최소 연료의 값"을 구하기 위해 모든 경우의 수를 따져보는 경우 O(N^3)이므로, 보자마자 DP로 풀어야 할 거 같은 느낌이 들었다!
나는 우선 각 방향에 번호를 붙여주었다. (k : 0 ~ 2)

다음으로 dp 배열의 의미를 다음과 같이 정의해 주었다.
dp[y][x][k] : dp[y][x][k] : 방법 k로 (y, x)에 도착할 때, 필요한 연료
이와 같은 방식으로 문제를 풀 때 DP 배열의 초기화가 필요하다.
예를 들어 dp[1][1][1]의 값이 dp[2][1][1]에 쓰일 수 없는데, ( = 같은 방향으로 두 번 연속 움직일 수 없음 )
초기화해주지 않으면, 0으로 초기화되어 있기 때문에, 해당 값을 최소 값으로 판단해서, 답이 0이 나올 수 있기 때문이다!!
나는 100*1000+1의 값으로 초기화를 해주었다.
#include<iostream>
#define MAX 1001
#define INF 100001
using namespace std;
int N, M;
int map[MAX][MAX];
int dp[MAX][MAX][3]; // dp[y][x][k] : 방법 k로 (y, x)에 도착할 때, 필요한 연료
void input(){
cin >> N >> M;
for (int y = 1; y <= N; y++){
for (int x = 1; x <= M; x++) {
cin >> map[y][x];
for (int k = 0; k < 3; k++) dp[y][x][k] = INF; // init for DP
}
}
}
void solution(){
for (int y = 1; y <= N; y++){
for (int x = 1; x <= M; x++){
if(x!=1) dp[y][x][0] = min(dp[y-1][x-1][1], dp[y-1][x-1][2]) + map[y][x];
dp[y][x][1] = min(dp[y-1][x][0], dp[y-1][x][2]) + map[y][x];
if(x!=M) dp[y][x][2] = min(dp[y-1][x+1][0], dp[y-1][x+1][1]) + map[y][x];
}
}
int ans = INF;
for (int x = 1; x <= M; x++) {
for (int d = 0; d < 3; d++)
ans = min(ans, dp[N][x][d]);
}
cout << ans;
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
input();
solution();
}시간 복잡도 비교
Brute-force : 행의 개수를 N, 열의 개수를 M이라고 하면, 각 행에서 3가지 방향을 모두 시도하므로 시간 복잡도는 대략 O(3^N) 정도
Dynamic Programming : O(N*M)
'문제 풀이 > 백준' 카테고리의 다른 글
| BOJ 9047번: 6174 (0) | 2023.12.11 |
|---|---|
| BOJ 2304번: 창고 다각형 (0) | 2023.09.05 |
| BOJ 2230번: 수 고르기 (0) | 2023.09.03 |
| BOJ 16928번: 뱀과 사다리 게임 (0) | 2023.08.29 |
| BOJ 1347번: 미로 만들기 (0) | 2023.08.08 |
