문제
문제 바로가기> BOJ 1238번: 파티
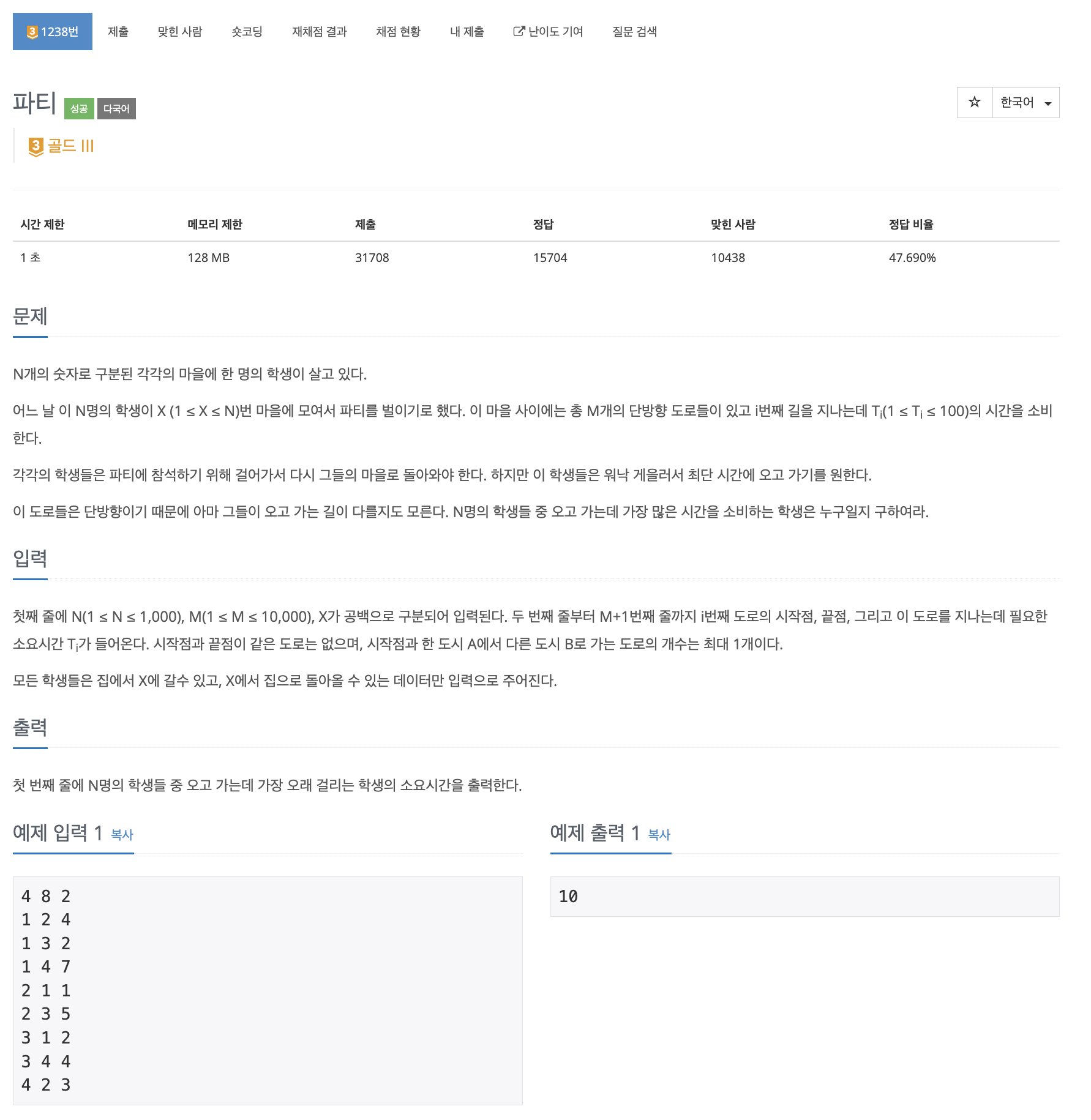
1238번: 파티
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어
www.acmicpc.net
풀이
파티가 열리는 마을에서 돌아오는 데 걸리는 최소 시간은 다익스트라 알고리즘으로 구할 수 있다!
하지만, 돌아오는 것은?!
그래프를 만들 때, 역방향 값을 저장해 놓고,
한 번 더 다익스트라 알고리즘을 이용하면, 파티가 열리는 마을에 가는 데 걸리는 최소 시간도 구할 수 있다!
#include<iostream>
#include<vector>
#include<queue>
#define MAX 1001
#define INF 987654321
using namespace std;
int N, M, X;
int dist[MAX], sum_dist[MAX];
vector<pair<int, int>> path[MAX], inverse_path[MAX];
void input(){
cin >> N >> M >> X;
int a, b, t;
for(int i=0; i<M; i++){
cin >> a >> b >> t;
path[a].push_back({b, t}); // 돌아오는 길 (X - > 다른 마을)
inverse_path[b].push_back({a, t}); // 가는 길 (다른 마을 -> X)
}
}
void dijkstra(vector<pair<int, int>> *v){
for(int i=1; i<=N; i++) dist[i] = INF; // init
priority_queue<pair<int, int>> pq;
pq.push({0, X}); // start point : X
dist[X] = 0;
while(!pq.empty()){
int now_node = pq.top().second;
int now_cost = -pq.top().first;
pq.pop();
for(int i=0; i<v[now_node].size(); i++){
int next_node = v[now_node][i].first;
int new_cost = dist[now_node]+v[now_node][i].second;
if(new_cost > dist[next_node]) continue;
dist[next_node] = new_cost;
pq.push({-new_cost, next_node});
}
}
for(int i=1; i<=N; i++) sum_dist[i]+=dist[i];
}
void solution(){
dijkstra(path);
dijkstra(inverse_path);
int ans = 0;
for(int i=1; i<=N; i++) ans = max(ans, sum_dist[i]);
cout << ans << "\n"; // N명의 학생들 중 오고 가는데 가장 오래 걸리는 학생의 소요시간
}
int main(){
ios_base::sync_with_stdio(0); cin.tie(0);
input();
solution();
}
'문제 풀이 > 백준' 카테고리의 다른 글
| BOJ 2178번: 미로 탐색 (1) | 2022.12.02 |
|---|---|
| BOJ 1260번: DFS와 BFS (0) | 2022.12.02 |
| BOJ 15591번: MooTube (Silver) (1) | 2022.12.02 |
| BOJ 2579번: 계단 오르기 (0) | 2022.11.30 |
| BOJ 12865번: 평범한 배낭 (0) | 2022.11.29 |
